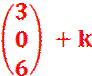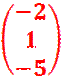Berechnungen bei Schnittproblemen zwischen geometrischen Objekten
über
die Lösung eines linearen Gleichungssystems nach der CRAMERschen Regel
1. Schnitt von zwei Geraden
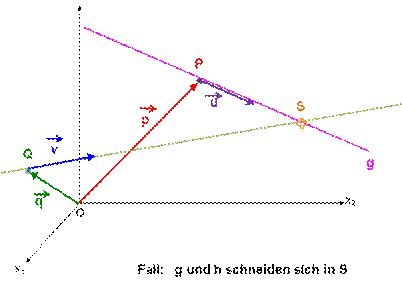
Allgemein
könnte man für den Fall, dass die beiden Richtungsvektoren ![]() und
und ![]()
keine Vielfachen voneinander sind den
Differenzvektor ![]() –
– ![]() bilden und diese
bilden und diese
drei
Vektoren auf lineare Abhängigkeit überprüfen:
B Beispiel r; s;
k Î
R0
![]()
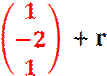
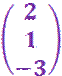
![]()
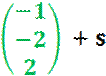
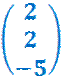
Es
ist:
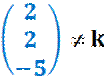
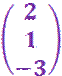
Untersuche
die Vektoren auf lineare Abhängigkeit/Unabhängigkeit:
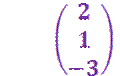
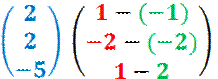
D = 0
also: Vektoren sind linear
abhängig und besitzen einen
Schnittpunkt S. [ Berechnet S
(-3/-4/7) ]
Für
den Fall, dass D ¹ 0 ist, wären die beiden Geraden
windschief.
1. Schnitt von Gerade und Ebene ( in
Parameterdarstellung )
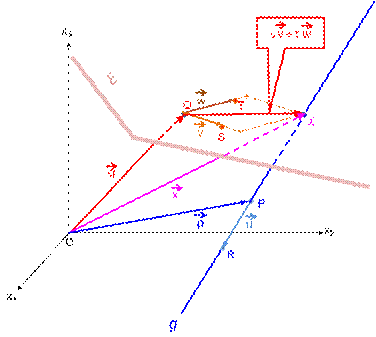
Beispiel r; s;
t Î
R0
![]()
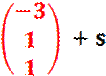
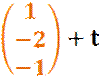
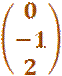
![]()
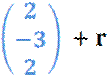
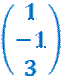
Nach
dem Gleichsetzen, Ordnen und Zusammenfassen ergibt sich
![]()
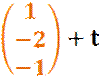
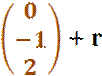
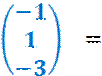
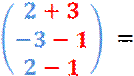
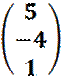
|
|
1 |
0 |
-1 |
|
|
|
|
D = |
-2 |
-1 |
1 |
= 6 |
|
|
|
|
-1 |
2 |
-3 |
|
|
|
|
|
1 |
0 |
5 |
|
|
Dr = |
-2 |
-1 |
-4 |
= -18 |
|
|
-1 |
2 |
1 |
|
und
damit kann in der Geradengleichung mit r = -18/6 = -3 bereits
der Schnittpunkt S berechnet werden: S ( -1 / 0 /-7 ) bzw./oder
über s
= 2 sowie t = -3 dann in der Ebenengleichung.
2. Schnitt von zwei Ebenen
Falls
die Ebenen in der Parameterdarstellung vorgegeben sind, sollten
diese
in die äquivalente Koordinatengleichung umgewandelt
werden…
Gewinnung
einer Koordinatengleichung aus der Parameterdarstellung
gelingt über die Nutzung entsprechender Determinanten.
Die Parametergleichung einer Ebene lässt sich wie folgt umformen:
E: ![]() =
= ![]() + r
+ r
![]() + s
+ s
![]() zu
zu ![]() -
- ![]() =
r
=
r ![]() + s
+ s
![]()
Aus
dieser Darstellung kann gefolgert werden, dass der eine Vektor ![]() -
- ![]()
sich
als Linearkombination der beiden anderen Vektoren darstellen lässt...
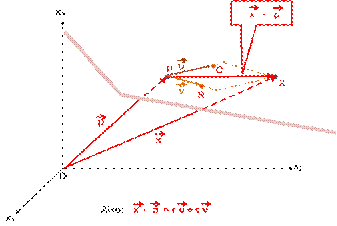
Dies bedeutet wiederum, dass die drei Vektoren
linear abhängig sein
müssen und daher gelten muss:
|
|
x1-p1 |
u1 |
v1 |
|
|
|
x2-p2 |
u2 |
v2 |
=
0 |
|
= 0 |
x3-p3 |
u3 |
v3 |
|
Die Auflösung dieser Determinante erbringt
letztlich die gewünschte
Koordinatengleichung der Ebene
mit einer Gleichung ax1 + bx2 + cx3
= d welche eine Ebene beschreibt,
falls die Koeffizienten a, b, c nicht alle 0
sind.
Beispiel :
![]()
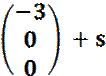
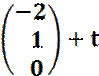
![]()
|
|
|
|
|
|
|
|
|
|
x1-3 |
-2 |
0 |
x1-3 |
-2 |
|
|
D = |
x2-0 |
1 |
0 |
x2-0 |
1 |
= 0 |
|
|
x3-0 |
0 |
1 |
x3-0 |
0 |
|
|
|
|
|
¯ x1-3 |
¯0
|
¯0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+[ (x1-3) ∙ 1∙ 1 ] +
[ (-2) ∙ 0 ∙ (x3-0)
] + [ 0 ∙ (x2-0) ∙ 0 ] = x1-3
|
|
|
|
|
0 |
0 |
2x2 |
|
|
x1-3 |
-2 |
0 |
x1-3 |
-2 |
|
|
D = |
x2-0 |
1 |
0 |
x2-0 |
1 |
= 0 |
|
|
x3-0 |
0 |
1 |
x3-0 |
0 |
|
|
|
|
|
|
|
|
|
-[ (x3-0) ∙ 1 ∙ 0 ] - [ 0 ∙
0 ∙ (x1-3) ] - [ 1 ∙ (x2-0) ∙ (-2) ] = 2x2
D = x1-3+2x2= 0 also: E1: x1
+ 2x2 =
3
Ebenso ergibt sich für E2
![]()
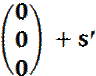
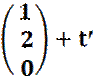
![]()
E2: 2x1
- x2 -
x3 = 0
Ermittlung von Schnittgeraden
E1: x1 + 2x2 = 3
bzw. E2: 2x1 - x2 - x3 = 0
Betrachtung von linearen Gleichungssystemen,
die aus den vorliegen-
den
Koordinatengleichungen entstehen
|
|
x1 |
+ 2x2 |
|
= 3 |
|
|
2x1 |
- x2 |
- x3 |
= 0 |
Einführung
einer in beiden Gleichungen vorhandenem Variablen als
Parameter
: x2 = k und
Betrachtung als Teil der Absolut-Glieder
|
|
x1 |
|
|
= 3 – 2k |
|
|
2x1 |
|
- x3 |
= 0 + k |
|
|
1 |
0 |
|
|
|
D = |
2 |
-1 |
= -1 |
|
|
|
|
|||
|
|
3-2k |
0 |
|
|
|
Dx1
= |
k |
-1 |
= -3+2k |
mit x1 = 3 - 2k
|
|
1 |
3-2k |
|
|
|
Dx3
= |
2 |
k |
= -6+5k |
mit x3 = 6 - 5k
Daraus
ergibt sich die Geradengleichung für die Schnittgerade g
![]()