Definition der ( mathematischen ) Funktion
Eine Zuordnung ist in der Mathematik eine Aktion, die zu jeder Größe einer Ausgangsmenge eine Größe einer Zielmenge zuweist.
Das Resultat aller solcher Zuordnungen heißt Abbildung.
Unter einer Funktion versteht man eine ( spezielle ) Zuordnung, die zu jeder Größe der Ausgangsmenge genau eine Größe einer Zielmenge zuweist. Dabei entsteht eine eindeutige Abbildung.
Demnach ist eine eindeutige Abbildung oder Funktion eine Beziehung zwischen zwei Mengen, die jedem
Element der einen Menge (
Funktionsargument, unabhängige Variable, x-Wert ) genau
ein Element der anderen Menge ( Funktionswert, abhängige Variable, y-Wert ) zuordnet, so
dass eine Menge geordneter Paare ( x I y )
entsteht.
Eine Funktion f ordnet
jedem Element x einer Definitionsmenge D ( auch Definitionsbereich ; Urbildmenge oder Urbild ) genau ein Element y einer
Wertemenge W ( auch Wertebereich oder Zielmenge ) zu. Schreibweise für eine vorgegebene Definitionsmenge D:
f: x ® y
.
Beachte: für das einzige, dem Element x Î D zugeordnete Element der Wertemenge schreibt man oft auch f(x) und somit auch die Darstellung f : x ® f(x)
Darstellungsmöglichkeiten für eine ( mathematischen ) Funktion
Eine Funktion ( Zuordnung ) kann
unter anderem in einer der folgenden Formen beschrieben werden:
Funktionsgleichung mit Definitionsmenge
Beispiel: f(x) = x2
+ 1 ;
x Î ![]()
Eindeutige Zuordnungsvorschrift mit Definitionsmenge
Beispiel: x ® x2 + 1 ; x Î ![]()
Wertetabelle
Beispiel:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
… |
|
|
2 |
5 |
10 |
17 |
26 |
37 |
50 |
… |
Als Menge geordneter Paare
insbesondere auch als aufgezählt oder beschrieben dargestellte Teilmenge
Beispiel:
f
= { ( 1 ½ 2 ) ; ( 2 ½ 5 ) ; ( 3 ½ 9 ) ; ( 4 ½ 16 ) ; … }
Anwendung der ( mathematischen ) Funktion in der Chemie
Beispiel:
LSG Zwischen der Stoffmenge n und der Masse m einer Stoffportion besteht eine anschauliche Beziehung:
Jeder konkreten Stoffmenge n wird genau eine Masse m
zugordnet, so dass eine Menge geordneter
Paare ( n I m ) entsteht.
f: n ® m
ist für n > 0 eine Funktion.
Zudem gilt je größer n, desto größer m.
Die Stoffmenge n und die Masse m einer Stoffportion sind
einander proportional.
>Wertetabelle für den Stoff Magnesium ( Mg ):
|
n(Mg) ( in mol ) |
1 |
1,5 |
2 |
2,5 |
3 |
|
m(Mg) ( in g ) |
24 |
36 |
48 |
60 |
72 |
>Graph für Mg : [ eigentlich für die Funktion m(Mg) = k · n(Mg) ]
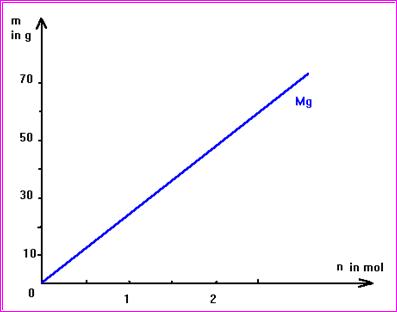
>Berechnung
des Proportionalitätsfaktors k für alle geordneten Paare ( n I m )
k = m : n = 24 g ∙
mol -1
Der Proportionalitätsfaktor heißt molare Masse M. Die
molare Masse M wird berechnet aus M = m : n.
Die Molare Masse kennzeichnet den Stoff als eine Konstante, aus dem eine Stoffprobe besteht.
> Beispiel: M (Mg) = 24 g ∙ mol -1
n = f(m) = M ∙ m ist eine proportionale Funktion.