Analytische Geometrie unter Nutzung von Matrizen und Determinanten

( ohne Verwendung von GTR )

1. Der Begriff „Matrix“

In der Mathematik stellt eine Matrix (Plural: Matrizen) eine einer Tabelle ähnliche rechteckige Anordnung von Elementen oder mathematischen Objekten dar, mit der man in bestimmter Weise rechnen kann ( Matrix-Addition, verschiedene Arten der Matrix-Multiplikation).

Matrizen sind vor allem ein grundlegendes Konzept der linearen Algebra. Sie stellen z.B. Zusammenhänge, in denen Linearkombinationen eine Rolle spielen, übersichtlich dar und erleichtern damit Rechen- und Gedankenvorgänge. Desweiteren werden insbesondere dazu benutzt, die in den verschiedenen Grundaufgaben entstehenden linearen Gleichungssysteme zu beschreiben. Zudem werden über die Matrizen lineare Abbildungen interpretiert.

Mögliche Definition

Eine rechteckige Anordnung von m ∙ n Zahlen a_ik in m Zeilen und n Spalten wird Matrix vom Typ

( m ; n ) genannt.

	a₁₁	a₁₂	…	a_1n
	a₂₁	a₂₂	…	a_2n
A =	a₃₁	a₃₂	…	a_3n
	:	:		:
	a_m1	a_m2	…	a_mn

Die Werte a_ik heißen Elemente von A.

Matrizen vom Typ ( 1 ; n ) heißen Zeilenvektoren.

Matrizen vom Typ ( m ; 1 ) heißen Spaltenvektoren.

Beispiele

>Koeffizientenmatrix für ein lineares Gleichungssystem, typisch für Probleme im sogenannten „Anschauungsraum“ sind die quadratischen Matrizen ( 3 ; 3 ) und die ( 3 ; 1 ) Vektoren als spezielle Matrizen

2

3

-1

A =

1

3

1

-2

-2

4

2x₁+ 3 für

(I)	2x₁	+3x₂	- x₃	= 1
(II)	x₁	+3x₂	+x₃	= 2
(III)	-2x₁	-2x₂	+4x₃	= 4

>Spaltenvektor der Absolutglieder bzw. erweiterte Koeffizientenmatrix

b =

®

2

-1

(A,b) = 1

-2

2. Der Begriff „Determinante“

In der linearen Algebra ist die Determinante eine spezielle Funktion, die einer quadratischen Matrix A eine reelle Zahl ( „Skalar“ ) det A ( meist auch D bzw. ½A½ ) zuordnet.

Für eine nur aus einem Koeffizienten bestehende (1 ; 1 ) - Matrix A ist

$\det A = \det \begin{pmatrix} a_{11} \end{pmatrix} = a_{11}.$

Ist A eine ( 2 ; 2 ) - Matrix, dann ist

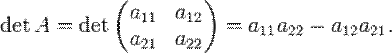
$\det A=\det \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = a_{11} a_{22} - a_{12} a_{21}.$

Für eine ( 3 ; 3 ) - Matrix A gilt die Formel

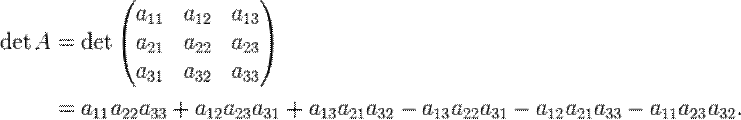
$\begin{align} \det A &= \det \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \\ &= a_{11} a_{22} a_{33} +a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{22} a_{31} - a_{12} a_{21} a_{33} - a_{11} a_{23} a_{32}. \end{align}$

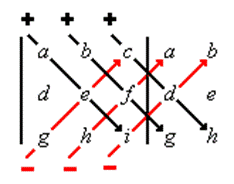
Will man diese Determinante von Hand berechnen, so stellt die Regel von SARRUS dafür ein einfaches Schema zur Verfügung:

Bei einer ( 3 ; 3 ) – Matrix besteht die Determinante aus 6 Summanden von je 3 Faktoren, die leicht mit dem folgenden Schema ermittelt werden können.

Dabei schreibt man die ersten beiden Spalten der Matrix rechts neben die Matrix und bildet Produkte von je 3 Zahlen, die durch die schrägen Linien verbunden sind. Dann werden die nach unten verlaufenden Produkte addiert ( Richtung der Hauptdiagonalen ) und davon die nach oben verlaufenden Produkte subtrahiert ( Richtung der Nebendiagonalen ).

Man erhält auf diese Weise die Determinante von A:

det(A) = aei + bfg + cdh − gec − hfa − idb.

[ Also dasselbe Ergebnis wie in der Formel oben dargestellt ! ]