Umgang mit affinen Abbildungen
Mit
Matrizen kann man ( ähnlich wie mit Vektoren ) bestimmte Rechenoperationen
ausführen
5.2. Addition und skalare Vervielfachung von
Matrizen
Definitionen:
Eine Matrix A wird mit einer reellen Zahl
r vervielfacht, indem man
jedes Element von A mit r multipliziert.
Kurz:
r ∙ A = r ∙ ( aik ) = (
r ∙ aik ) [ heißt
r – faches der Matrix A ]
Zwei Matrizen B und C vom Typ ( m ; n ) werden addiert, indem man
die
in den Matrizen an entsprechender Stelle stehenden Elemente addiert.
Kurz:
B + C = ( bik ) + ( cik ) = ( bik
+ cik
) [ heißt Summe ]
Multiplikation von Matrizen
Es gilt dabei
folgende Voraussetzung:
Eine
Multiplikation zweier Matrizen ist ausführbar, wenn folgende
Verknüpfungsbedingung erfüllt ist:
Ein Produkt A ∙ B existiert, wenn
die Anzahl der Spalten von A
mit der Anzahl der Zeilen von B übereinstimmt.
Allgemeiner
Fall: Multiplikation einer Matrix mit einer Matrix
Definition:
Eine Matrix A vom Typ ( m ; n ) und eine
Matrix vom Typ ( n ; k )
werden multipliziert, indem man jeweils
das Skalarprodukt des
entsprechenden Zeilenvektors mit jedem
Spaltenvektor bildet.
Es entsteht dabei eine Matrix vom Typ ( m ;
k ).
Beispiel
· 
= 
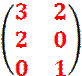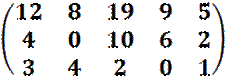
LV >meist wird das sogenannte FALKsche Schema benutzt
|
|
|
2 |
0 |
5 |
3 |
1 |
|
|
|
3 |
4 |
2 |
0 |
1 |
|
3 |
2 |
12 |
8 |
19 |
9 |
5 |
|
2 |
0 |
4 |
0 |
10 |
6 |
2 |
|
0 |
1 |
3 |
4 |
2 |
0 |
1 |
Also 3
* 2 + 2 * 3 = 12 usw.
LS
Spezieller Fall: Multiplikation
einer Matrix mit einem Vektor
Definition:
Eine Matrix A vom Typ ( m ; n ) und ein
Vektor c mit n Koordinaten
[also eine Matrix vom Typ ( n ; 1 )] werden multipliziert, indem man
n- mal jeweils das Skalarprodukt
des entsprechenden Zeilenvektors
mit dem vorgegebenen Vektor bildet.
Es entsteht dabei ein Vektor mit m
Koordinaten.
Beispiel
· 
= 
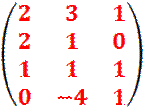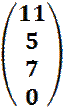
LSG
LV >hier wird wieder das sogenannte FALKsche Schema benutzt
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
4 |
|
2 |
3 |
1 |
11 |
|
2 |
1 |
0 |
5 |
|
1 |
1 |
1 |
7 |
|
0 |
-4 |
1 |
0 |
Also
2 * 2 + 3 * 1 + 1 * 4 = 11
usw.
Als
eine mögliche Anwendung ermöglicht die Multiplikation von Matrizen die
Herstellung
spezieller linearer Abbildungen
Definition
Eine
Zuordnung über Abbildungsgleichungen der Form
x1‘
= a1x1 + a2x2 + c1
x2‘
= a3x1 + a4x2 + c2
heißt
affine Abbildung.
Andere
Schreibweise mit einer Abbildungsmatrix und Verschiebungsvektor
= 
· 
+ 
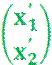Beispiel mit bekannter Abbildungsmatrix ohne Verschiebung
D ( 2 / 3 ) D‘ ( -4 / -3 )
· 
= 
LV >hier wird wieder das sogenannte FALKsche Schema benutzt
|
|
|
|
|
|
|
3 |
|
|
-2 |
|
|
0 |
-1 |
-3 |
Evt. in einer geometrischen Figur als Schrägspiegelung
Punkt C' ( -3 ; -3 ) Punkt D ( 2 ; 3 ) Punkt D' ( -4 ; -3 )
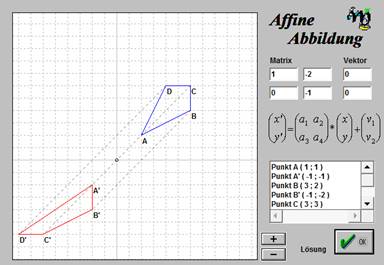
Beispiel mit zu bestimmender Abbildungsmatrix ( ohne Verschiebung )
bei bekannter Zuordnung
A ( 1 / 5 ) A‘ ( 3 / 5,5 ) und
B ( 2 / 2 ) B‘ ( -2 / 3 )
· 
= 
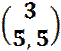
LV >hier wird wieder das sogenannte FALKsche Schema benutzt und ein lineares Gleichungssystem gelöst:
|
|
|
|
|
|
|
5 |
|
|
b |
|
|
c |
d |
5,5 |
LV
Also a * 1 + b * 5
= 3 oder
a + 5b = 3 I *
(-2)
c + 5d = 5,5 I * (-2)
2a + 2b = -2
2c + 2d = 3
Führt zu:
-2a - 10b = -6
-2c - 10d = -11
2a + 2b = -2
2c + 2d = 3 ergibt nach der Addition -8b = -8 und -8d = -8
Also b = 1 ; d = 1 ;
a = -2 ; c = 0,5 als Elemente der Abbildungsmatrix